Machine Learning Note - Convex Optimization

11 November 2019

Introduction

I’ve been taking an online Machine Learning class recently. This post is my note on convex optimization part.

Contents

Optimization

1. Overview

  • AI problem = Model + Optimization (Similar to Program = Data Structure + Algorithm)
  • Models: DL, LR, SVM, XGBoost, NN, RL
  • Optimization: GD/SGD, Adagrad/Adam, Newton’s, L-BFGS, Coordinate Descent, EM.

2. Standard Form

Any optimization problem can be represented as the following standard form:

\[\begin{align} Minimize \ \ \ & f_0(x) \\ s.t. \ \ &f_i(x)\le 0, \ \ i={1,...,K}\\ & g_j(x)=0, \ \ j={1,...,L} \\ \end{align}\]

Examples:

  • Linear Regression:
\[\sum_{i=1}^{n}(w^Tx_i - y_i)^2+\|w\|^2_2 \\ \|Xw-Y\|^2_2 + \|w\|^2_2\]
  • Logistic Regression:
\[\sum_{i=1}^{n}(y_ilog\sigma(w^Tx_i+b) + (1-y_i)log(1-\sigma(w^Tx_i+b))\]
  • Support Vector Machine:
\[\|w\|^2_2 + \lambda\sum_{i=1}^{y}\epsilon_i\\ s.t. \ \ \epsilon_i \ge 1-y_i(w^Tx_i+b)\]
  • Collaborative Filtering:
\[\sum_{(i,j)\in\Omega} (u^T_i v_j-r_{ij})^2 + \lambda\|u\|^2_F + \gamma\|u\|^2_F\]
  • K-Means
\[\sum_{i=1}^{n}\ \sum_{k=1}^{K} \gamma_{ik}\|x_i - \mu_k\|^2_2\\ \gamma_{ik}= \begin{cases} 1, \ \ \ if \ x_i \in k^{th} \ cluster,\\ 0, \ \ \ otherwise. \end{cases}\]

3. Categories

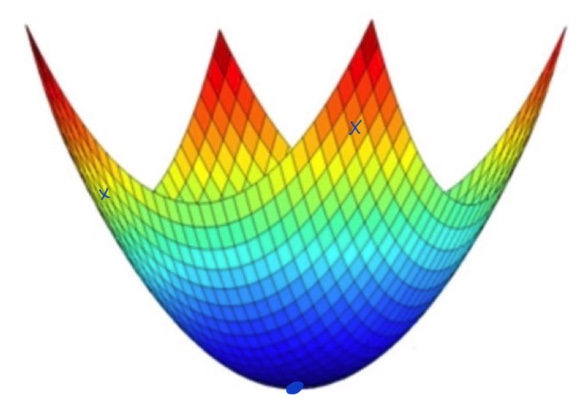
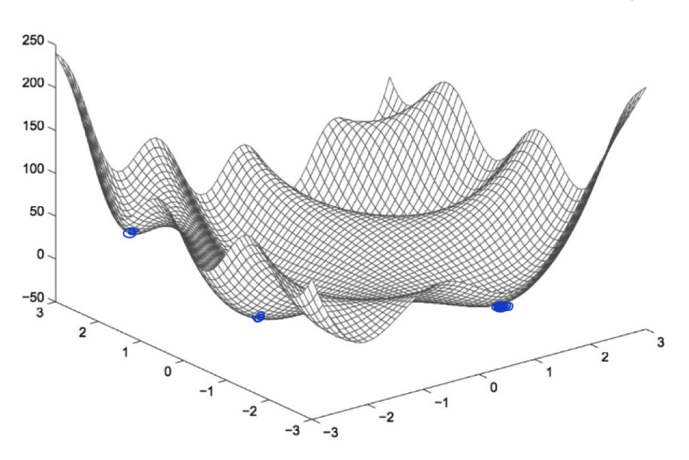
  1. Convex vs Non-Convex
  2. Continuous vs Discrete
  3. Constrained vs Unconstrained
  4. Smooth vs Non-smooth

Solving a non-convex optimization problem:

  1. For some simple function, we can use brute-force search to validate all feasible solutions.
  2. Relax some constrains and convert the problem to a convex function.
  3. Directly solving the problem using a optimization algorithm, try to find a better local optimal.
Convex function has a unique global optimal.
Convex function has a unique global optimal.
 Non-convex function has a more than one local optimals.
Non-convex function has more than one local optimals.

Convex Optimization

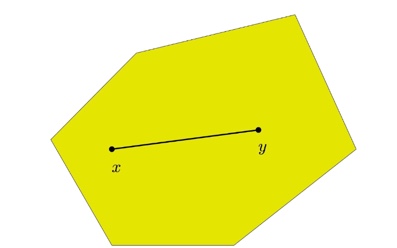
1. Convex Set:

$\forall x,y \in C, \forall a \in [0, 1].$ $C$ is a convex set if $ax+(1-a)y\in C$ .

An example of convex set
An example of convex set

Convex Set VS Non-Convex Set:

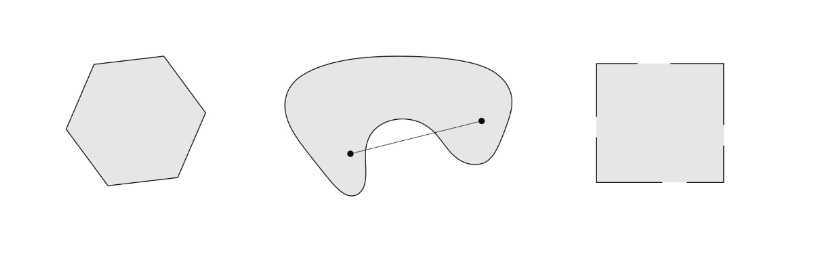
Left: Convex, Middle: Non-Convex, Right: Non-Convex

Examples of Convex Set:

  • $R^n$
  • Positive Integers $R^n_+$
  • Norm $|x| \le 1$
  • Affine set: All solution of a linear equation set $Ax = b$.
  • Halfspace: All solution of a inequality $Ax \le b$.

Theroem: Intersection of convex sets is convex.

2. Convex Function

2.1 Definition

Definition. Let $X$ be a convex set in a real vector space and let $f:X\to R$ be a function.

  • $f$ is called convex if: \(\forall x_1, x_2 \in X, \forall t \in [0, 1]: f(tx_1+(1-t)x_2\le tf(x_1)+(1-t)f(x_2)\)
  • $f$ is called strickly convex if: \(\forall x_1\neq x_2 \in X, \forall t \in [0, 1]: f(tx_1+(1-t)x_2\le tf(x_1)+(1-t)f(x_2)\)
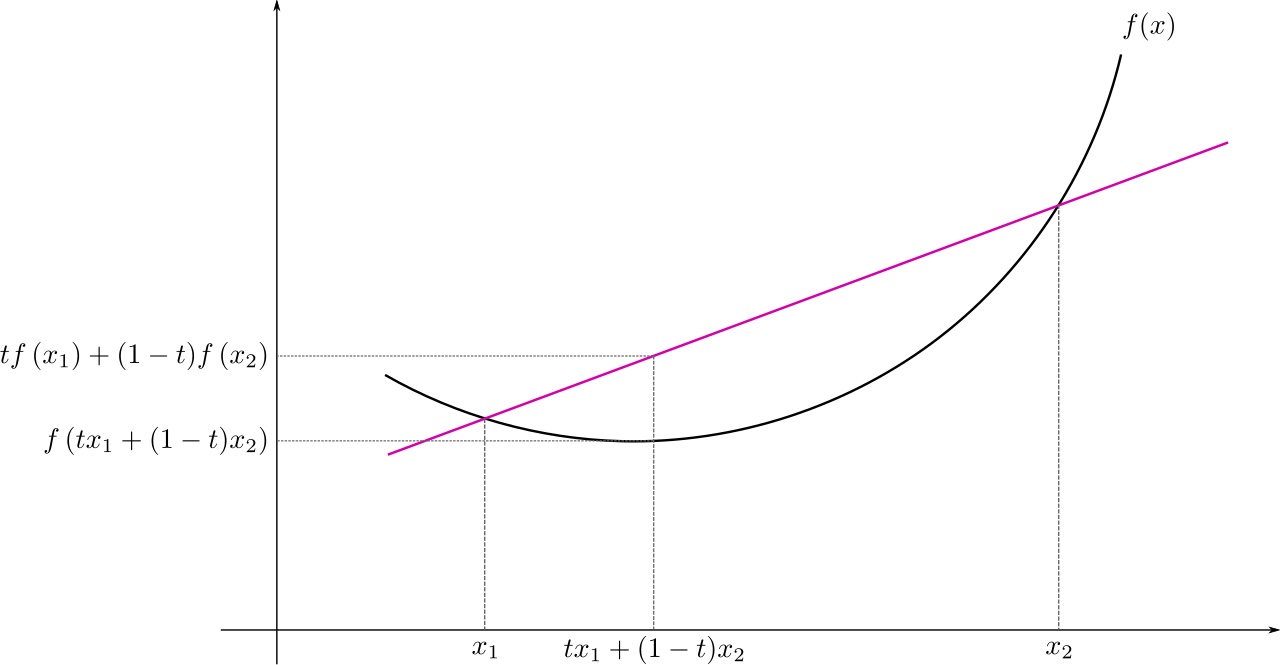
Illustration of the convex definition.

Property: Summation of convex functions is convex function.

2.2 First Order Convexity Condition

Theorem. Suppose $f: R^n \to R$ is differentiable. Then, $f$ is convex $\iff f(y)\ge f(x)+\nabla(x)^T(y-x), \forall x, y \in dom(f).$

First order convexity condition.
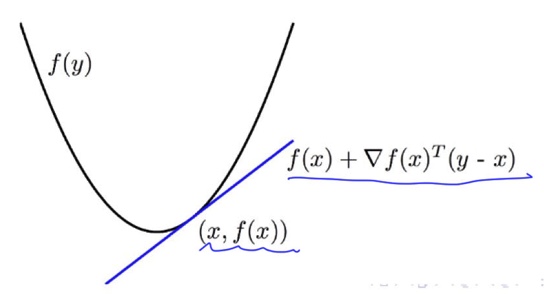
2.3 Second Order Convexity Condtion

Theorem. Suppose $f: R^n \to R$ is twice differentiable. Then $f$ is convex $\iff \nabla^2f(x)\succeq0, \forall x \in dom(f).$

Note that we use $\succeq$ (succeeds or equals) here instead of $\ge$ (greater than or equals). $A\succeq0$ means that $A$ is a positive semi-definite (PSD) matrix. (i.e.; all of the eigenvalues of $A$ are positive.

3. Proof of Convexity

Example 1. Prove that Linear Function: $f(x)=b^Tx + c$ is convex.

Proof: By definition, $\forall x_1, x_2 \in dom(f)$, we have:

\[\begin{align} b^T(tx_1+(1-t)x_2)+c &\le t(b^Tx_1+c) + (1-t)(b^Tx_2 + c)\\ tb^Tx_1+(1-t)b^Tx_2+c &\le tb^Tx_1+tc + (1-t)b^Tx_2 + (1-t)c\\ c &\le tc + (1-t)c\\ c &\le c \end{align}\]

The inequality holds, hence the linear function $f(x)=bTx+c$ is convex.

Example 2. Prove that qualdratic function: $f(x)=\frac{1}{2}x^TAx + b^Tx + c, \forall A\succeq 0 \ $ is convex.

Proof: We will use second order convexity condition.

Let $\nabla$ be the partial derivative operator $\frac{\partial}{\partial x}$

\[\frac{\partial f}{\partial x} = \nabla f = Ax + b \\ \frac{\partial^2 f}{\partial^2 x} = \nabla^2f = A\]

Since $A\succeq 0$, $\nabla^2f$ is a positive semi-definite matrix. Thus, the qualdratic function is convex.

Example 3. Prove that p-norm is convex. \(\|x\|_p=(\sum_{i=1}^{n}\|x_i\|^p)^{1/p}\).

Proof: Let \(f(x)=\|x\|_p\), using Minkowski inequality (triangle inequality), we have:

\[\|\lambda x_1+(1-\lambda)x_2\|_p \le \|\lambda x_1\|_p + \|(1-\lambda) x_2\|_p = \lambda\| x_1\|_p + (1-\lambda)\| x_2\|_p\]

So by definition, p-norm is convex.

Example 4. Prove that logistic regression loss is convex. \(L(w)=-\sum_{n=1}^{N}(y_nlog(p_n) + (1-y_n)log(1-p_n)\)

where: \(p_n = \frac{1}{1+e^{-W^Tx_n}}\)

Proof: We will the second order convexity condition to prove this.

Let $\nabla$ denotes partial derivative operator $\frac{\partial}{\partial w}$

\[\begin{align} \nabla p&=\nabla \frac{1}{(1+e^{-{W^Tx}})} \\ &=-\frac{1}{(1+e^{-{W^Tx}})^2} \nabla(1+e^{-{W^Tx}}) \\ &=-\frac{1}{(1+e^{-{W^Tx}})^2} e^{-{W^Tx}} \nabla(-w^Tx) \\ &=-\frac{1}{(1+e^{-{W^Tx}})^2} e^{-{W^Tx}}\cdot(-x) \\ &=\frac{e^{-{W^Tx}}}{(1+e^{-{W^Tx}})^2} \cdot x \\ &=\frac{1}{(1+e^{-{W^Tx}})}\frac{e^{-{W^Tx}}}{(1+e^{-{W^Tx}})} \cdot x \\ &=\frac{1}{(1+e^{-{W^Tx}})}\frac{1+e^{-{W^Tx}}-1}{(1+e^{-{W^Tx}})} \cdot x \\ &=\frac{1}{(1+e^{-{W^Tx}})}(1-\frac{1}{(1+e^{-{W^Tx}})}) \cdot x \\ &=p(1-p)x \end{align}\]

Now we can calculate the first order derivative:

\[\begin{align} \frac{\partial L(w)}{\partial w} &=\nabla{L(w)} \\ &=-\sum_{n=1}^{N}(y_n\nabla log(p_n) + (1-y_n)\nabla log(1-p_n)) \\ &=-\sum_{n=1}^{N}(y_n \frac{1}{p_n}\nabla p_n + (1-y_n)\frac{1}{1-p_n}\nabla (1-p)) \\ &=-\sum_{n=1}^{N}(y_n \frac{p_n(1-p_n)}{p_n}x_n + (1-y_n)\frac{-p_n(1-p_n)}{(1-p_n)}x_n) \\ &=-\sum_{n=1}^{N}(y_n(1-p_n)x_n - (1-y_n)p_nx_n) \\ &=-\sum_{n=1}^{N}(y_n - y_np_n - p_n + y_np)x_n \\ &=-\sum_{n=1}^{N}(y_n-p_n)x_n \\ &=\sum_{n=1}^{N}(p_n-y_n)x_n \end{align}\]

Now we calculate the second order derivative:

\[\begin{align} \frac{\partial^2 L(w)}{\partial^2 w} &=\sum_{n=1}^{N}\nabla((p_n-y_n)x_n) \\ &=\sum_{n=1}^{N}\nabla(p_nx_n) \\ &=\sum_{n=1}^{N}(p_n(1-p_n)x_n{x_n}^T) \end{align}\]

Then, we need to prove that matrix $p_n(1-p_n)x_n{x_n}^T$ is PSD:

\[\begin{align} \forall v\in \mathcal{R} v^THv &= v^Tp_n(1-p_n)x_n{x_n}^Tv \\ &= p_n(1-p_n)(x_n^Tv)^2 \\ \end{align}\]

Since $p_n$ is a sigmoid function, we have $p_n(1-p_n) \geq 0$, which leads to $v^THv \geq 0$.

Thus, H is PSD and we proved that the logistic regression loss is a convex function.

Note: To prove a matrix $H$ is PSD, we need to prove that $\forall v\in R, v\neq0, v^THv \ge0.$