Paper Summary: From Word Embeddings To Document Distances
13 November 2019
Paper Title: From Word Embeddings To Document Distances
Conference: ICML2015
Link:http://proceedings.mlr.press/v37/kusnerb15.pdf
1. 简介
如何衡量两个Document之间的距离一直是Information Retrival里的一个热门问题。之前主要的方法是用Bag of words (BOW)或者TF-IDF的方法去计算,但是这两种方法的局限在于它们有Frequent Near-orthogonality的性质。简单来说就是某些语义上相近的文档可能在这些方法下会得到一个非常大的距离。
文章里用了一个例子,考虑如下两个不同文档中的句子:
- Obama speaks to the media in Illinois
- The President greets the press in Chicago.
可以看到这两个句子其实从语义上非常接近,但是因为它们没有Common words, 用BOW或者TF-IDF会直接得到maximum distance。
为了改进这个问题,这篇文章提出了一种新的距离度量 Word Mover’s Distance (WMD)。作者在设计这个distance的时候引入了最近word embedding的一些新成果,使得方法能够考虑到词之间的语义距离。
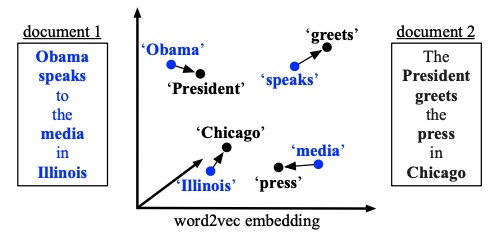
词向量
这里简单回顾一下Word2Vec,这种方法顾名思义就是将字典中的任意单词转换为一个向量。Word2Vec有一个比较好的性质就是在Word Embedding空间里的距离和实际上的语义距离非常贴近。比如Obama和President这两个单词在向量空间里就很接近。Word2Vec的两外一个性质是在Embedding Space里的向量操作会保留语义关系。举个例子,我们知道柏林是德国的首都,而巴黎是法国的首都,那么在词向量空间里Vec(柏林) - Vec(德国) + Vec(法国) $\approx$ Vec(巴黎)。
2. Word Mover’s Distance
首先假设我们已经有一个提前训练好的word2vec embdding matrix $X\in \mathcal{R}^{d\times n}$。其中 $n$ 是这个我们字典里单词的个数。这个 矩阵的每一列 $x_i\in\mathcal{R}^d$ 是一个长度为 $d$ 的向量,表示了字典里第 $i$ 个词所对应的向量。
2.1 文档表征
接下来,我们可以将一个document表示成一个归一化后的 $n$ 维nBOW向量,即 $d\in\mathcal{R}^n$。 这里的 $n$ 同样是字典的大小。向量里的每一个scalar是该词在文档中出现的次数除以字典中所有词出现的总次数(类似于词频)。比如我们假设字典里的第 $i$ 个词在文档中出现了 $c_i$ 次,那么 $d_i=\frac{c_i}{\sum^n_{j=1}c_j}$。
这种文档的表示方法实际上可以看作是构造了一个 $n-1$ 维的单纯形(simplex),而一个文档的表征向量 $d$ 可以看作这个单纯形上的一个点。如果两个文档没有任何common words,那它们的表征向量 $d$ 则会出现在单纯形上的两个不连通平面上。但是实际上它们在语义上可能会很相似,也从另一个角度上说明了之前方法的局限性。
2.2 文档距离
作者引入word2vec,定义两个单词的在词向量空间的欧式距离作为这两个单词之间的travel cost,即 $c(i, j) = |x_i - x_j|_2$。这里的 $c$ 和上边那个 $c_i$ 应该没有关系。
假设我们要衡量两个文档 $d$ 和 $d’$ 的距离,首先我们允许 $d$ 中的每个词向 $d’$ 中的任意一个词转换,作者定义一个转换矩阵 $T\in\mathcal{R}^{n\times n},\ T_ij\ge0$ 用来描述 $d$ 中的每个单词向 $d’$ 中每个单词的转换程度。
比如文档1中的media这个词,可以转换为文档2里这四个词的任意一个词 (president,greets,press, Chicago),转换的程度可调,比如0.2, 0.5, 0.3, 0.1. (随便举个例子)。然后我们最终会通过去优化这个转换矩阵 $T$ 来实现目标函数最小。
为了保证文档 $d$ 完全被转换成 $d’$,作者加了一个限制保证每个词outgoing flow加起来等于 $d_i$. 即 $\sum_jT_{ij} = d_i$。
同时也要保证 $d’$ 中每个词的输入流正好等于 $d_i’$ 即 $\sum_iT_{ij}=d_j’$。这里个人理解成为了避免 $d$ 大量词都被转换为 $d’$ 中的某个特定词。
最终,我们可以定义两个文档的距离WMD为:
\[WMD=\sum_{i,j}T_{ij}c(i,j)\]优化这个距离实际上是一个Transportation problem,可以写成如下LP问题:
\[\begin{align} \min_{T\ge0} \ \ \ &\sum_{i,j=1}^nT_{ij}c(i,j) \\ s.t. \ \ \ & \sum_{j=1}^nT_{ij} = d_i \ \ \ \forall i\in\{1, ...,n\} \\ & \sum_{i=1}^nT_{ij} = d'_j \ \ \ \forall j\in\{1, ...,n\} \end{align}\]这个LP问题可以用很多已有的方法来解,这里不再赘述。
另外作者在文中给了一个直观的图解(下图),可以看到在两个句子没有任何common words的情况下,WMD还是比较好的给出了它们之间的距离。
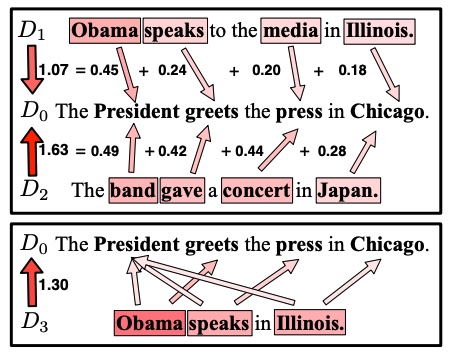
3. Fast Distance Computation
WMD算法本身的复杂度是 $O(p^3logp)$ (p是文档中不重复单词的个数),当我们要比较的文档比较多的时候,这个计算量可能会比较高从而限制了实际使用。为了解决这个问题作者给出了几个原距离的relaxation。
3.1 Word Centroid Distance.
两个文档的Word Centroid Distance(WCD) 定义为它们的加权平均向量之间的欧式距离,即:
\[WCD = \|Xd-Xd'\|\]作者在文中用三角不等式证明了WCD是WMD的一个lower bound。计算这个距离的复杂度是 $O(dp)$。好处是在实际中可以快速的计算出来,缺点是这个lower bound不够tight。
3.2 Relaxed Word Moving Distance
考虑到精度问题,作者在文章中提了另外具有tighter的bound的relaxation,这两个relaxation是通过分别relax原LP问题的两个constraint得到的。
通过移除第二个constraint,优化问题变为:
\[\begin{align} \min_{T\ge0} \ \ \ &\sum_{i,j=1}^nT_{ij}c(i,j) \\ s.t. \ \ \ & \sum_{j=1}^nT_{ij} = d_i \ \ \ \forall i\in\{1, ...,n\} \\ \end{align}\]因为任一满足原来两个constraint的解必然也是现在松弛后的问题的一个解,我们可以看出松弛后的问题必然是原问题的lower-bound。
另一方面,这个松弛后的优化问题的最优解可以直接得出,即将每个词都转换为离它最近的一个词:
\[T^*_ij= \begin{align} \begin{cases} d_i, \ \ &if \ \ j = argmin_jc(i,j) \\ 0, \ \ &otherwise. \end{cases} \end{align}\]因此,在实际求解的时候只需要计算 $j = argmin_jc(i,j)$。
同样的,通过移除第一个constraint,我们能得到另一个原问题的lower-bound。这样在实际使用的时候,我们可以通过取 $max(l_1(d, d’), l_2(d, d’))$ 来得到一个更tight的bound。
实验
作者在8个不同的benchmark上做了kNN classification的测试,结果达到了state-of-the-art的效果。同时也对比了几个不同的relaxation的效果,发现提出的RWMD确实能得到比WCD更tight的bound。
Critics
- 做了relaxation之后感觉计算成本可能在实际应用中还是偏高,如果是类似搜索引擎这种对百万千万级别的文档量做比较,可能开销还是有点大。
- WMD是一个距离度量,但是似乎并没有解决把文档转换为特征向量的问题。往这个方向做的话有可能能够同时解决聚类和分类之类的下游问题。相当于如果能够拿到一个好的文档embedding的话,就可以直接做embedding的比较,以及把这个embedding接到很多下游任务上。